Truncation Error

강좌: 수치해석

Taylor 급수

Taylor 급수는 수치해석에서 매우 근본적인 이론을 제공한다.

Taylor 정리

함수 \(f\)와 그것의 처음 \(n+1\)차까지의 미분이 \(a\)와 \(x\)를 포함하는 구간에서 연속적이라면, \(x\)에서의 함수 값은 다음과 같이 주어진다.

\[\begin{split} \begin{align} f(x) = f(a) &+ f'(a)(x-a) + \frac{f''(a)}{2!}(x-a)^2 \\ &+ \frac{f^{(3)}(a)}{3!}(x-a)^3 + ... \\ &+ \frac{f^{(n)}(a)}{n!}(x-a)^n + R_n \end{align} \end{split}\]

여기서 나머지 \(R_n\) 은 다음과 같이 정의된다.

\[ R_n = \int_a^x \frac{(x-t)^{n+1}}{n+1!} f^{(n+1)} dt. \]

다음 중간간 정리에 따르면 \(\xi \in [a, x]\) 에 대해서 아래 식을 만족한다.

\[ \int_a^x g(t)dt = g(\xi)(x-a). \]

이를 적용하면 \(R_n\) 은 다음과 같다.

\[ R_n = \frac{(x-a)^{n+1}}{n+1!} f^{(n+1)}(\xi) = \frac{h^{n+1}}{n+1!} f^{(n+1)}(\xi). \]

여기서 \(h=x - a\) 이다.

Taylor 급수를 이용한 근사화

Taylor 급수를 이용하면 비선형 함수를 근사적으로 계산할 수 있다.

예제: \(e^x\) 함수 근사화

\(e^x\) 함수를 원점 \((a=0)\) 에서 다항식으로 근사화해보자.

\[ e^x \approx 1 + x + \frac{x^2}{2} + \frac{x^3}{3!} +... + \frac{x^n}{n!} \]

%matplotlib inline
from matplotlib import pyplot as plt

import numpy as np

plt.style.use('ggplot')
plt.rcParams['figure.dpi'] = 150

def factorial(n):
    """ Factorial 계산
    Parameters
    ----------
    n : integer
        n
    """
    fac = 1
    for i in range(1, n+1):
        fac *= i
        
    return fac


def approx_exp(n, x):
    """ Exponential 함수 근사
    Parameters
    ----------
    n : integer
        항의 계수
    x : float
        값
    """    
    exp = 0
    for i in range(n):
        exp += 1/factorial(i)*x**i
    
    ## Pythoniac
    # exp = sum([factorial(i)*x**i for i in range(n)])
    return exp

x = np.linspace(-1, 1, 101)

# Plot approximation
for i in range(2, 5):
    plt.plot(x, approx_exp(i, x))

# Plot exact    
plt.plot(x, np.exp(x), color='black')

# Legend
plt.legend([
    '1st order approximation',
    '2nd order approximation',
    '3rd order approximation',
    'Exact ($e^x$)'
])

# Label
plt.xlabel('x')
plt.ylabel('y')

Text(0, 0.5, 'y')

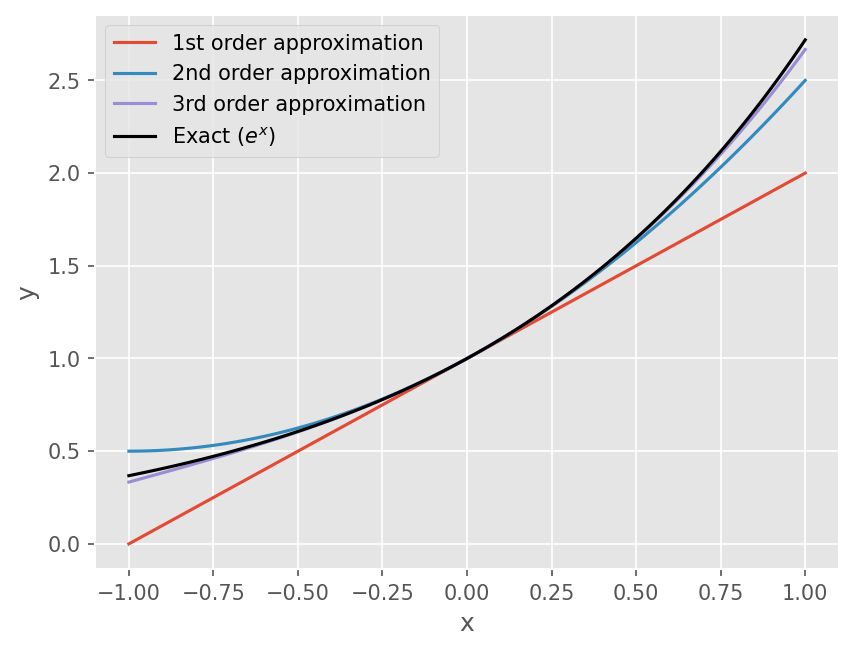
전단오차 (Truncation error)

Taylor 급수를 이용한 근사식의 경우 n차 항까지만 사용하므로 그 이상의 항은 절삭 (Truncation) 한다. 이에 따른 오차를 전단오차 (Truncation Error)라 한다.

위 예제에서 \(x=0.5\) 일 때 절대오차를 계산하면 다음과 같다.

x = 0.5
exact = np.exp(x)

for i in range(2, 5):
    approx = approx_exp(i, x)
    error = exact - approx
    
    print("Error using {}-th order terms: {:.5e}".format(i-1, error))

Error using 1-th order terms: 1.48721e-01
Error using 2-th order terms: 2.37213e-02
Error using 3-th order terms: 2.88794e-03

x 크기를 바꿔가면서 그래프로 그려보면 아래와 같다.

x = np.linspace(1e-3, 0.1, 100)
exact = np.exp(x)

# Plot error between approximation and exact values
for i in range(2, 5):
    approx = approx_exp(i, x)
    error = exact - approx
    
    plt.loglog(x, error)
    
# Same scale of x and y
plt.axis('equal')

# Legend
plt.legend([
    '1st order approximation',
    '2nd order approximation',
    '3rd order approximation',
])

plt.xlabel('x')
plt.ylabel('$\epsilon$')

Text(0, 0.5, '$\\epsilon$')

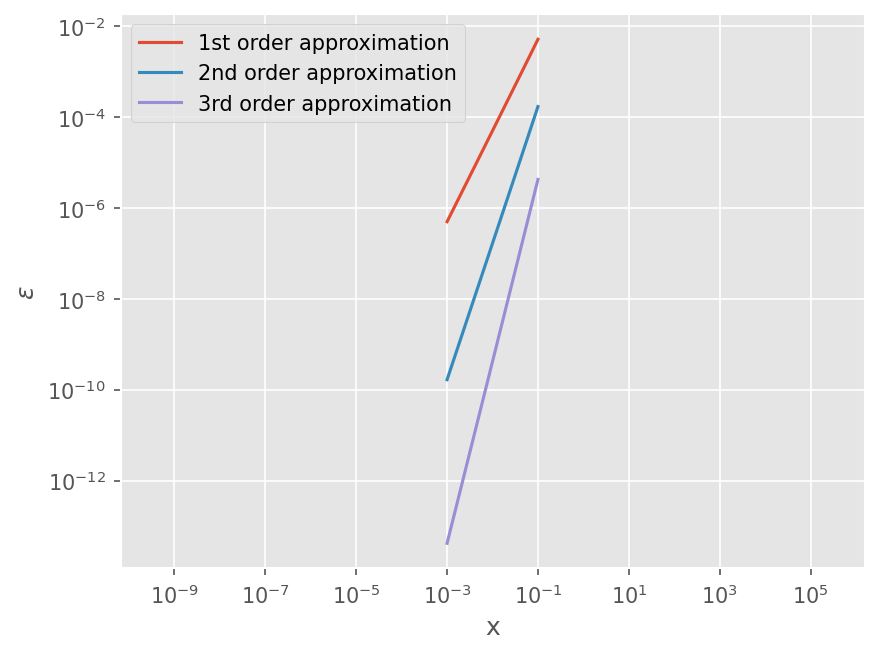
오차항 \(R_n = C h^{n+1}\) 이므로 log scale 로 그렸을 때 기울기가 \(n\) 이다.

즉 아래 그래프를 보면 기울기가 각각 2, 3, 4차임일 알 수 있다.

오차항을 다음과 같이 표현하기도 한다.

\[ R_n = O(h^{n+1}) \]

DIY

\(\sin(x)\) 를 \(a=\pi/4\) 를 기준으로 Taylor series를 이용하여 근사식을 구하고, \([0, \pi/2]\) 구간에서 근사해와 이론해를 비교하시오. 전단오차의 크기를 확인하시오.

오차의 전파

함수의 오차

실제 공학 문제에서는 다양한 오차가 발생한다. 예를 들어 계측하는 과정에서 오차가 있을 수 있고, 이론식에서 가정에 의한 오차가 있을 수 있다. 특히 수치해석 과정에서는 Round-off error, Truncation error 등이 존재한다.

독립변수 \(x\)에 대해서 오차가 있어서 근사값 \(\tilde{x}\)을 사용하는 경우를 생각하자. 이때 함수 \(f(x)\) 결과의 오차는 다음과 같다.

\[ \Delta f(\tilde{x}) = |f(x) - f(\tilde{x})| \]

Taylor expansion을 이용하면

\[ f(x) = f(\tilde{x}) + f'(\tilde{x})(x - \tilde{x}) + \frac{f''(\tilde{x})}{2} (x - \tilde{x})^2 + ... \]

1차 항으로만 근사하면 함수 \(f(x)\) 결과의 오차는 다음과 같다.

\[ \Delta f(\tilde{x}) \approx |f'(\tilde{x})| \Delta \tilde{x} \]

예제

근사값 \(\tilde{x}=2.5\) 이고 이 값에 0.01의 오차가 있다. 이 경우 함수 \(f(x)=x^3\) 계산시 발생하는 오차를 구해보자.

위 근사식을 적용하면

\[ \Delta f(\tilde{x}) \approx |f'(\tilde{x})| \Delta \tilde{x} = 3(2.5)^2 0.01 = 0.1875 \]

즉 오차는 다음과 같이 정리할 수 있다.

\[ f(x) = f(\tilde{x}) \pm \Delta f(\tilde{x}) = 15.625 \pm 0.1875 \]

다변함수의 경우 편미분을 이용한 Taylor expansion을 활용한다.

\[ f(x, y) \approx f(\tilde{x}, \tilde{y}) + \frac{\partial f}{\partial x} \Delta \tilde{x} + \frac{\partial f}{\partial y} \Delta \tilde{y} + O(\Delta \tilde{x}^2, \Delta \tilde{y}^2) \]

Condition Number

수학에서 조건은 입력값의 변화에 대한 민감도이며, 작은 입력 오차에 따라 함수의 변화가 클수록 불안정해질 수 있다.

Condition Number는 독립변수의 상대오차 대비 함수의 상대오차로 정의한다.

\[ Cond = \frac{\epsilon_{a, f(x)}}{\epsilon_{a, x}} \]

각각의 상대오차는 다음과 같다.

\[\begin{split} \begin{align} \epsilon_{a, x} &= \frac{\Delta \tilde{x}}{\tilde{x}} \\ \epsilon_{a, f(x)} & = \frac{\Delta f(\tilde{x})}{f(\tilde{x})} \approx \frac{|f'(\tilde{x})| \Delta \tilde{x}}{f(\tilde{x})} \end{align} \end{split}\]

Condition Number는 다음과 같다.

\[ Cond = \frac{\frac{|f'(\tilde{x})| \Delta \tilde{x}}{f(\tilde{x})}}{\frac{\Delta \tilde{x}}{\tilde{x}}} = \frac{\tilde{x} f'(\tilde{x})}{f(\tilde{x})} \]

Condition Number가 큰 경우 작은 오차에도 함수가 매우 크게 바뀌므로 수치해석시 조심해야 한다. 이런 함수를 ill-conditioned라 한다.

예제

\(\tan(\tilde{x})\)의 Condition Number는 다음과 같다.

\[ Cond = \frac{\tilde{x} f'(\tilde{x})}{f(\tilde{x})} = \frac{\tilde{x} 1/\cos^2(\tilde{x})}{\tan{\tilde{x}}} \]

즉 \(\tilde{x} =\pi/4, \pi/2\times0.999\) 에서 Condition Number는 다음과 같다.

x = np.pi/4

Cond = x * 1/np.cos(x)**2 /np.tan(x)
Cond

1.5707963267948963

x = np.pi/2*0.999

Cond = x * 1/np.cos(x)**2 /np.tan(x)
Cond

999.0016432910481

x = np.linspace(-np.pi/2, np.pi/2, 101)[1:-1]
plt.plot(x, np.tan(x))

plt.xlabel("x")
plt.ylabel("y")

plt.legend(["$tan(x)$"])

<matplotlib.legend.Legend at 0x7fdb6e8f6b50>

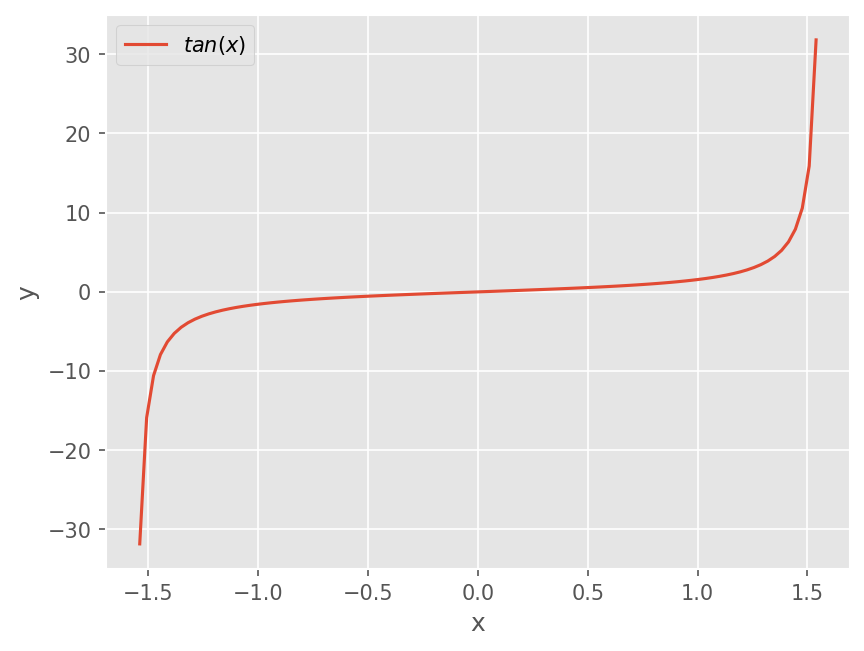
전체 수치 오차

복습하면 수치 오차는 다음 두 가지로 구성된다.

• Round-off Erorr: 숫자 표기 한계로 반올림에 의한 오차

• Truncation Error: 계산 과정에서 절단애 의한 오차

수치 해석에서는 2가지를 유의해야 한다.

• Consistency: 수치 오차는 가급적 적어야 한다.

• Stability: 발생한 수치 오차가 증폭되지 않아야 한다.